Enlarging a Drawing & Squaring Off

Adrian Scott Stokes (British, 1854-1935) Autumn in the Mountains tempera on canvas 31 1/2 X 42 in.

The other day, I grabbed the book Practical Landscape Painting by Adrian Stokes from my shelf, and as I leafed through it, I was struck by two things:  1.  artists used to go through a lot of string, and 2. Stokes was right:  what a student may or may not know should never be taken for granted.  Though this information from Stokes on the enlarging of working surfaces and the gridding-up of sketches is rather basic, perhaps it is still good to record the information here, nonetheless.

When the necessary sketches and studies have been painted, and the drawings in black and white, from nature, have also been done, the proportions of the canvas, on which the picture is to be painted, must be decided.  These may be determined by making a careful drawing of the composition of the subject on a paper of moderate size, a large margin being left all round to allow extension of the drawing in any direction.  No pains should be spared in the attempt to make this drawing represent as accurately as possible the final combination of all that has been learnt about the subject. 

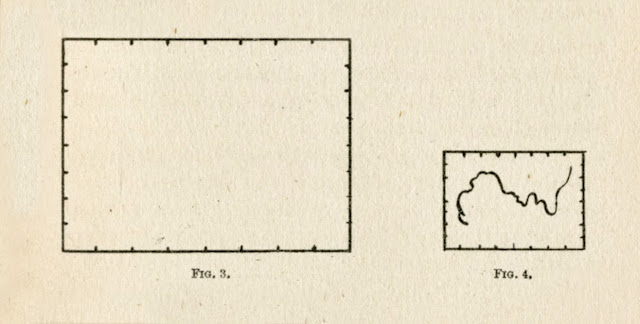
When the drawing is done, and either the length, or the height, of the canvas has been decided on, a simple plan for finding the other dimension is as follows :  Lay the drawing on a rectangular table, with two sides of it coinciding with those of the table, and then draw a diagonal line with a thread, from corner to corner, and prolong it.

Any two lines, such as those marked with dots in Fig. 2, drawn parallel to the sides of the drawing, which meet at the thread, inclose a space having the same proportions as those of the drawing.  For example, if the canvas has the length of A to B, a perpendicular line drawn from B meets the thread at C, and a line parallel to AB that meets the perpendicular line at D, gives the required length of AD. A "rule of three" sum will, of course, easily solve the problem, but as it does not show the actual dimensions, it is not so effective.

My readers will, I hope, excuse me if I seem to under-rate their intelligence ;  my excuse is that I have met with quite advanced students who were ignorant of any means for enlarging work, in due proportions.

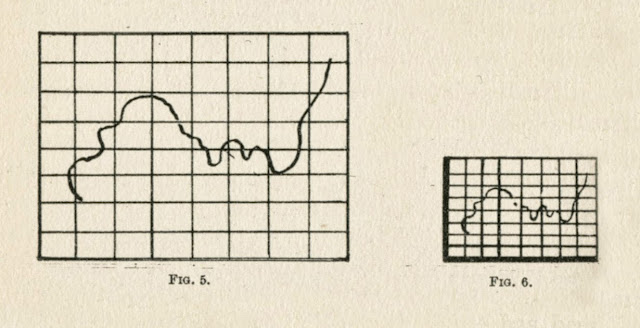
The process known as squaring "off" comes next.  It consists of dividing drawing, and canvas, into an equal number of similar small spaces, and copying what is in each.  The simplest plan is to divide both sides of the drawing, and canvas, into two equal parts, to divide those again, and again.  If the drawing is very elaborate, many "squares" will be needed ;  if it is simple, fewer will suffice. 

Pins put into the points thus marked, and black cotton drawn horizontally, and vertically, on both drawing and canvas, will define the relative spaces on each.

When that which is in each space has been copied, either with charcoal or in paint, and the threads are removed, the first stage of the work will be found to be satisfactory and correct. 

But the satisfaction then felt is, unfortunately, generally destined to be short-lived.  Difficulties will soon be encountered, which evoke feelings from hope to despair ;  complete satisfaction rarely comes again.

Jean-Léon Gérôme (French, 1824-1904) Pelt Merchant of Cairo, 1869 (detail) Once a drawing and the canvas have been gridded, corresponding squares can be further segmented into smaller shapes where detail is most important.